Finding the missing number

Solution:
-Ignore the middle numbers (3,5,8,8,?)
- Add the side numbers and divide by 2
- You will get the middle number as answer!

 Solution:

4(3)2= [4+2 /2 = 3]

5,3(5)1,1= [5+3+1+1 /2 = 5]

6,1,2(8)3,3,1= [6+1+2+3+3+1 /2 = 8]

7,2(8)4,3= [7+2+4+3 /2 = 8]

9(?)3= [9+3 /2 = 6]

Mixed Again

Simplification

Simplify:
$\frac{3}{4} + \frac{2}{3} - \frac{1}{2}$

Solution:
LCM of 4, 3, 2 = 12
= (9 + 8 − 6)/12 = 11/12

✅ Answer: 11/12

---

Square Root and Cube Root

Find the cube root of 27 × 125.

Solution:
27 = 3³, 125 = 5³ → 27×125 = (3×5)³ = 15³
∛(27×125) = 15

✅ Answer: 15

---

Surds and Indices

Simplify:
$\sqrt{50} + \sqrt{18}$

Solution:
√50 = √(25×2) = 5√2
√18 = √(9×2) = 3√2
Sum = (5 + 3)√2 = 8√2

✅ Answer: 8√2

---

Ratio and Proportion

Divide Nu. 3,600 between Choki and Dema in the ratio 5:7.

Solution:
Total parts = 12
Choki = (5/12)×3600 = Nu. 1,500
Dema = (7/12)×3600 = Nu. 2,100

✅ Answer: Choki = Nu. 1500, Dema = Nu. 2100

---

Chain Rule

If 5 workers can build a wall in 12 days, how many days will 8 workers take to build the same wall?

Solution:
More workers → less time
New time = (5×12)/8 = 7.5 days

✅ Answer: 7.5 days

---

Pipes and Cistern

A pipe fills a tank in 6 hours, another empties it in 9 hours. If both work together, how long to fill the tank?

Solution:
Net rate = 1/6 − 1/9 = (3−2)/18 = 1/18
Time = 18 hours

✅ Answer: 18 hours

---

Boats and Streams

Karma rows upstream 24 km in 6 hours and returns downstream in 3 hours. What is the speed of the stream?

Solution:
Upstream speed = 24/6 = 4 km/h
Downstream = 24/3 = 8 km/h
Speed of stream = (8 − 4)/2 = 2 km/h

✅ Answer: 2 km/h

---

Alligation or Mixture

Mix sugar at Nu. 40/kg with sugar at Nu. 60/kg to get 50 kg at Nu. 50/kg. How much of each is needed?

Solution:
Cheaper → 60 − 50 = 10
Costlier → 50 − 40 = 10
Ratio = 1:1 → 25 kg each

✅ Answer: 25 kg of each

---

Logarithm

If log₁₀2 = 0.3010, find log₁₀8.

Solution:
log₁₀8 = log₁₀(2³) = 3×log₁₀2 = 3×0.3010 = 0.9030

✅ Answer: 0.9030

---

Races and Games

Pema beats Sonam by 20 meters in a 200 m race. When Sonam runs 200 m, how far has Pema run?

Solution:
Pema's speed : Sonam's = 200 : 180 = 10 : 9
When Sonam runs 200 m, Pema = (10/9)×200 = 222.22 m

✅ Answer: ~222 meters

---

Stocks and Shares

A 10% stock is bought at 90. Find the yield.

Solution:
Yield = (Dividend / Market Price) × 100 = (10 / 90)×100 = 11.11%

✅ Answer: 11.11%

---

Probability

A card is drawn from a deck. What’s the probability it’s a queen or a heart?

Solution:
P(queen) = 4/52
P(heart) = 13/52
P(both queen & heart) = 1/52
So: 4 + 13 − 1 = 16 → 16/52 = 4/13

✅ Answer: 4/13

---

True Discount

True discount on Nu. 600 due in 6 months at 10% p.a.?

Solution:
TD = (P × R × T) / (100 + (R×T))
= (600 × 10 × 0.5) / (100 + 5) = 3000 / 105 = Nu. 28.57

✅ Answer: Nu. 28.57

---

Banker’s Discount

Banker’s Discount on Nu. 1,200 due in 1 year at 6% p.a.?

Solution:
BD = (P×R×T)/100 = 1200×6×1 /100 = Nu. 72

✅ Answer: Nu. 72

---

Odd Man Out and Series

Find the odd one out:
3, 5, 11, 14, 17, 21

Solution:
All except 14 are prime.

✅ Answer: 14 (not prime)

ALL Mixed

Pema is 4 years older than Deki. After 6 years, the sum of their ages will be 40. What are their current ages?

Let Deki = x → Pema = x + 4
(x + 6) + (x + 4 + 6) = 40
x + 6 + x + 10 = 40 → 2x + 16 = 40 → x = 12
Deki = 12, Pema = 16

✅ Answer: Pema = 16 years, Deki = 12 years

Calendar

If 5th April 2025 is a Saturday, what day will 5th April 2026 be?

Solution:
2025 is not a leap year → adds 1 day
Saturday + 1 = Sunday

✅ Answer: Sunday

---

Clock

At what time between 2 and 3 o’clock will the hands of the clock be at a right angle?

Solution:
Right angle = 90°
Angle between hands = |(30×H − (11/2)×M)|
Between 2 & 3 → H = 2
So: |60 − 5.5M| = 90
Case 1: 60 − 5.5M = 90 → M = −5.45 ❌
Case 2: 5.5M − 60 = 90 → 5.5M = 150 → M = 27.27 minutes

✅ Answer: At approximately 2:27

---

Average

The average age of 5 friends is 16. If Sonam joins the group, the average becomes 17. What is Sonam’s age?

Solution:
Total of 5 = 5×16 = 80
New total = 6×17 = 102
Sonam = 102 − 80 = 22 years

✅ Answer: 22 years

---

Area

Find the area of a triangle with base 14 cm and height 12 cm.

Solution:
Area = ½ × base × height = ½ × 14 × 12 = 84 cm²

✅ Answer: 84 cm²

---

Volume and Surface Area

A cylindrical water tank in Mongar has a radius of 7 m and height of 4 m. Find the volume. (Use π = 22/7)

Solution:
Volume = πr²h = 22/7 × 7 × 7 × 4 = 616 m³

✅ Answer: 616 m³

---

Permutation and Combination

How many 3-letter codes can Kinley form using the letters A, B, C, D if no letter repeats?

Solution:
P(4,3) = 4 × 3 × 2 = 24

✅ Answer: 24 codes

---

Numbers

The sum of two numbers is 150. If one number is 20% more than the other, find the numbers.

Solution:
Let smaller = x → larger = 1.2x
x + 1.2x = 150 → 2.2x = 150 → x = 68.18
Other = 150 − 68.18 = 81.82

✅ Answer: 68.18 and 81.82

---

Problems on Numbers

A number when divided by 7 leaves remainder 4. When the same number is divided by 5, the remainder is 1. What is the smallest such number?

Solution:
Let number be x
x ≡ 4 mod 7 → x = 7a + 4
Now, 7a + 4 ≡ 1 mod 5 → 7a ≡ −3 ≡ 2 mod 5 → a = 4
x = 7×4 + 4 = 32

✅ Answer: 32

---

Problems on H.C.F. and L.C.M.

The H.C.F. of two numbers is 16, and their L.C.M. is 240. If one number is 48, find the other.

Solution:
HCF × LCM = a × b
16 × 240 = 48 × x → x = (16×240)/48 = 80

✅ Answer: 80

Time, Work and interest mixed

 Time and Work

Kezang can complete a job in 12 days, and Ugyen in 18 days. They work together for 4 days. How much work is left?

Solution:
Kezang = 1/12, Ugyen = 1/18
Together per day = (1/12 + 1/18) = 5/36
In 4 days: 4 × 5/36 = 20/36 = 5/9
Work left = 1 − 5/9 = 4/9

✅ Answer: 4/9 of the work remains

---

Simple Interest

Sonam deposited Nu. 12,000 at 6% simple interest for 3 years. What is the total interest?

Solution:
SI = (P × R × T) / 100 = (12000×6×3)/100 = Nu. 2,160

✅ Answer: Nu. 2,160

---

Compound Interest

Jigme invested Nu. 5,000 at 10% compound interest annually for 2 years. What is the compound interest?

Solution:
Amount = P(1 + R/100)^T = 5000(1.1)^2 = 5000 × 1.21 = Nu. 6,050
CI = 6050 − 5000 = Nu. 1,050

✅ Answer: Nu. 1,050

---

Profit and Loss

Dema bought oranges for Nu. 1,200 and sold them for Nu. 1,560. What was her profit percentage?

Solution:
Profit = 1560 − 1200 = 360
Profit% = (360/1200) × 100 = 30%

✅ Answer: 30% profit

---

Partnership

Kinley and Karma invested Nu. 10,000 and Nu. 15,000 respectively in a business. After 8 months, they made a profit of Nu. 9,200. What is Kinley’s share?

Solution:
Ratio = 10,000×8 : 15,000×8 = 10:15 = 2:3
Kinley’s share = 2/5 × 9200 = Nu. 3,680

✅ Answer: Nu. 3,680

---

Percentage

Pelden's salary increased from Nu. 12,000 to Nu. 14,400. What is the percentage increase?

Solution:
Increase = 2400 → % = (2400/12000)×100 = 20%

✅ Answer: 20% increase

Time and Distance mixed

 1. Problems on Trains

A train 180 meters long crosses Kinley standing on a platform in 9 seconds. It then crosses a 420-meter-long bridge in 24 seconds. What is the speed of the train in km/h?

Solution:
Let speed = x m/s
Length of train = 180 m
Time to cross bridge = (180 + 420)/x = 24 → 600/x = 24 → x = 25 m/s
Convert to km/h: 25 × 18/5 = 90 km/h

✅ Answer: 90 km/h

______________________________________________________________________________________________________________________________________________________________________

2. Time and Distance

Pema drove from Trongsa to Bumthang at 60 km/h and returned at 40 km/h. What is the average speed for the whole journey?

Solution:
Average speed = 2ab / (a + b) = 2×60×40 / (60+40) = 4800/100 = 48 km/h

✅ Answer: 48 km/h

______________________________________________________________________________________________________________________________________________________________________

3. Height and Distance

From a point 40 m away from the base of the Tashichho Dzong, Sonam observes the top at an angle of 45°. What is the height of the Dzong?

Solution:
tan(45°) = h/40 → 1 = h/40 → h = 40 meters

✅ Answer: 40 meters

Mixed Post

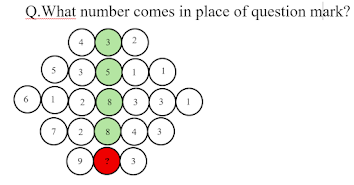
Q. Choden’s Train Trouble

A train 150m long crosses a bridge in 30 seconds at 36 km/h. Find the length of the bridge.

Solution:
Speed = 36 km/h = 10 m/s
Distance = Speed × Time = 10 × 30 = 300 m
Bridge length = 300 − 150 = 150 m

Answer: 150 meters

---

Q.Sangay’s Geometry Problem

The perimeter of a rectangle is 48 cm, and its length is 4 cm more than its width. Find dimensions.

Solution:
2(l + w) = 48 → l + w = 24
l = w + 4 → w + 4 + w = 24 → 2w = 20 → w = 10 → l = 14

Length: 14 cm, Width: 10 cm

---

Q.Dema’s Age Puzzle

Dema is twice as old as her sister now. 6 years ago, she was 3 times older. What are their ages?

Solution:
Let sister = x, Dema = 2x
6 years ago: 2x − 6 = 3(x − 6)
2x − 6 = 3x − 18 → x = 12 → Dema = 24

Dema: 24 years, Sister: 12 years

---

Q.Pema’s Investment (Simple Interest)

Pema invested Nu. 8,000 at 5% per annum for 3 years. What is the total interest?

Solution:
SI = (8000 × 5 × 3)/100 = Nu. 1,200

Answer: Nu. 1,200

---

Q.Karma's Cylinder Volume

Find the volume of a cylinder with radius 7 cm and height 10 cm. (π = 22/7)

Solution:
V = πr²h = 22/7 × 7 × 7 × 10 = 1540 cm³

Answer: 1540 cm³

---

Q.Phub’s Voting Math

In a village, 60% of 1,200 people voted. 70% of those voted for Kinley. How many votes did Kinley get?

Solution:
Votes cast = 60% of 1200 = 720
Kinley's = 70% of 720 = 504 votes

Answer: 504 votes

---

Q.Choki’s Percent Confusion

A number is increased by 20% and then decreased by 25%. What is the net % change?

Solution:
Let number = 100
Increase → 120
Decrease → 120 − 30 = 90
Change = 90 − 100 = −10%

Answer: 10% decrease

---

Q.Ugyen's Compound Interest

Ugyen deposited Nu. 10,000 at 10% compound interest for 2 years. Find the final amount.

Solution:
A = P(1 + r/100)^n = 10000(1.1)^2 = 10000 × 1.21 = Nu. 12,100

Answer: Nu. 12,100

---

Q.Lhamo’s Speed Puzzle

Lhamo drove from Mongar to Bumthang at 60 km/h and returned at 40 km/h. What was her average speed?

Solution:
Average speed = 2ab/(a + b) = 2×60×40 / (60+40) = 4800/100 = 48 km/h

Answer: 48 km/h

---

Q.Wangchuk’s Profit Ratio

Wangchuk sold a bicycle for Nu. 3,000, making 25% profit. What was the cost price?

Solution:
CP = SP / (1 + profit%) = 3000 / 1.25 = Nu. 2,400

Answer: Nu. 2,400

---

Q.Sangay’s Equation Mystery

Solve:
$(2x - 3)/5 = (x + 1)/3$

Solution:
Cross-multiply: 3(2x − 3) = 5(x + 1)
6x − 9 = 5x + 5 → x = 14

Answer: x = 14

---

Q.Kezang's Remainder Question

What is the remainder when 7⁴ is divided by 5?

Solution:
7⁴ = 2401
2401 ÷ 5 = 480 remainder 1

Answer: 1

---

Q.Namgay’s Area Puzzle (Trapezium)

A trapezium has bases 8 cm and 12 cm, and height 6 cm. Find its area.

Solution:
Area = ½ × (sum of bases) × height = ½ × (8+12) × 6 = ½ × 20 × 6 = 60 cm²

Answer: 60 cm²

---

Q.Tshering’s Ratio Challenge

Tshering and Dema share Nu. 800 in the ratio 3:5. How much does each get?

Solution:
Total parts = 3 + 5 = 8
Tshering = (3/8) × 800 = 300
Dema = (5/8) × 800 = 500

Answer: Tshering = Nu. 300, Dema = Nu. 500

---

Q.Pempa’s Clock Problem

At what time between 3 and 4 o’clock will the hands of the clock be at right angles?

Solution:
Angle = 90°
Formula: θ = |(30H − 11/2)M|
At 3:00 → Hour angle = 90°
Use: 90 = |90 − 11/2 M| → Solve
90 = 90 − 11/2 M → M = 0
or 90 = 11/2 M → M = 16.36

Answer: At 3:16 and 3:49 approx.

Mixed Labeled

 Q. Sonam’s Exam Puzzle (Algebra)

Sonam scored 5 marks more than twice what Pema scored in an exam. If their total score is 95, what did each score?

Solution:
Let Pema's marks = x
Then Sonam's marks = 2x + 5
x + 2x + 5 = 95
3x + 5 = 95 → 3x = 90 → x = 30
Sonam = 2(30) + 5 = 65

Pema: 30 marks, Sonam: 65 marks

---

Q. Tashi's Farm (Profit & Loss)

Tashi bought 100 kg of potatoes at Nu. 25/kg and sold 60 kg at 30/kg, but the rest spoiled. What is his profit/loss %?

Solution:

• Cost price = 100 × 25 = Nu. 2500

• Selling price = 60 × 30 = Nu. 1800

• Loss = 2500 − 1800 = 700
  Loss % = (700 ÷ 2500) × 100 = 28%

Answer: 28% loss

---

Q.Leki’s Number Riddle

The sum of two numbers is 45, and their difference is 13. What are the numbers?

Solution:
Let the numbers be x and y
x + y = 45
x − y = 13
Add: 2x = 58 → x = 29 → y = 16

Numbers: 29 and 16

---

Q.Jigme’s Time and Work

Jigme can finish a project in 15 days, and Pema in 20 days. How long will they take if they work together?

Solution:
Work/day: Jigme = 1/15, Pema = 1/20
Together = 1/15 + 1/20 = (4 + 3)/60 = 7/60
Time = 60/7 ≈ 8.57 days

Answer: ~8.57 days

distance and time

Q.Kinley rows a boat from Sarpang to Gelephu, a distance of 36 km. The river current is 3 km/h. His rowing speed in still water is 9 km/h. What is the time taken to go upstream and return?

Solution:

• Upstream speed = 9 − 3 = 6 km/h

• Downstream speed = 9 + 3 = 12 km/h

• Time upstream = 36 ÷ 6 = 6 hrs

• Time downstream = 36 ÷ 12 = 3 hrs

• Total time = 9 hours

Answer: 9 hours

Proft and loss

Q.Sonam bought 50 oranges from Gelephu at Nu. 10 per orange. She sold them in her village for Nu. 15 each. She spent Nu. 100 on transportation. What was her total profit?

Solution:

• Cost Price = 50 × 10 = Nu. 500

• Selling Price = 50 × 15 = Nu. 750

• Profit = Selling Price − Cost Price − Transport

• Profit = 750 − 500 − 100 = Nu. 150

Answer: Sonam earned a profit of Nu. 150

Average

Kinley hiked to Taktsang Monastery. It took him 3 hours to climb up and 2 hours to come down. If the total distance (up and down) is 12 km, what was his average speed for the whole trip?

Solution:

• Total distance = 12 km

• Total time = 3 hours (up) + 2 hours (down) = 5 hours

• Average speed = Total distance ÷ Total time = 12 ÷ 5 = 2.4 km/h

Answer: Kinley’s average speed was 2.4 km/h

མིང་དང་འབྲལ་བའི་ཞེ་ས།

Q.70% of Bumthaps speak Sharchop and 60% speak Khengkha. What is the minimum percentage of Khengkha-speaking Bumthaps that also speak Sharchop?

Solution Steps:

Use the formula: Min overlap = (A% + B%) - 100%

Min % = (70 + 60) - 100 = 30%

Tip:

✔ When dealing with overlaps, use Venn Diagram principles.

Arrangement

QKarma is heavier than Sonam. Dorji weighs less than Sonam. Dawa is heavier than Dorji but lighter than Sonam. Which of the following statements is NOT true?

A. Karma weighs more than Dorji

Photo by Harrison Haines

 

B. Sonam weighs less than Karma
C. Dorji weighs more than Karma
D. Dorji is the lightest of all.

Solution Steps:

From the given:

- Karma > Sonam
- Sonam > Dawa > Dorji

• This implies: Karma > Sonam > Dawa > Dorji

So:

A. Karma > Dorji → True

B. Sonam < Karma → True

C. Dorji > Karma → False (Dorji is the lightest)

D. Dorji is the lightest → True

Tip:

·        ✔ Arrange people visually or with symbols (K > S > D > Do) to avoid confusion.

Time calculation

 Q.  If it’s 3:00 PM in Tokyo and Tokyo is 3 hours ahead of Thimphu, what time is it in London? Assume London is 6 hours behind Thimphu.

Solution Steps:

Tokyo(3pm)- Thimphu(3pm-3 hours as Thimphu is 3 hours behind Tokyo-> so it is 12:00pm) 

Now as of London it is 6hours Behind Thimphu lo. Therefore, 12:00pm - 6 hours = 6am

Now the time at London is 6:00am.

Tip:

✔ Work backward time zone differences logically.

Sequencing

Photo by Alex Andrews: https://www.pexels.com/photo/phases-of-the-moon-1983032/

  Q. Next number in the sequence: 2, 12, 1112, 3112, 132112, 1113122112, ?

Solution:

This is a look-and-say sequence.

for example (2)- there is one number of digit two so-> 12

now for (12)- there is one number of digit 1 and one number of digit 2->1112

Each term describes the previous term's digits.

After 1113122112 → next is 311311222112

In words: there are three 1 and one 3, one 1 and two 2, two 1 and one 2.

Why Bhutan remained politically not unified till 16th century

1.Visit of religious missionaries:

From the 9th century onwards, many enlightened religious personages played varied roles in the lives of the Bhutanese people and the growth of their distinctive national identity. 

2. Busy propagating Buddhism than political unification:

Hinayana and Mahayana Buddhism practitioners were sent as a missionary in the Himalayan region; They were more focused on the spread of Buddhism in the region than a political overview.

3. Clashes between different sects of Buddhism.

 

Advent of Buddhism

The chronicled history of the Kingdom, 

however, begins with the advent of Buddhism 

in the 8th century –the arrival of  Guru   

Padmasambhava in 746 AD.

Some historians argue that Buddhism 

reached Bhutan before the arrival of Guru 

Rinpoche Probably in the 7th Century.

Bhutan-only nation in the world that has 

remained a sovereign independent country 

throughout its recorded history which goes 

back to the 7th century A.D

Bhutan: Evolution of Names

Sanskrit word ‘Bhotanta’, which means the end (anta) of Tibet (Bhot).

RI Drag Gi Yul (the country of mountainous terrain): people were called 

Rig Drag pa.

Menjong Norbuling (precious land of Medicinal herbs): a Sakya lama, 

10th century A.D.

Tsenden Mengyi Jong: (the land of abundant Cypress trees)

Druk Yul ( the land of thunder Dragon): Derived from Kargyu sect of 

Mahayana Buddhism  (now state Religion of Bhutan)

Evolution of Democracy in Bhutan.

National Assembly (1953)

•       Representative government.
•       Constitutional monarchy.
•       Involve people in decision making.
•      Develop a politically conscious society.

1968-surrendered his veto power.

RAC (1965)

•        Advised the King and Ministers.
•     Final court of appeal on the recommendation of the king.

Voices of people heard through their representatives.

Council of Ministers (1968).

• Executive power-sharing.

Separation of Judiciary (1968). 

  ·         High Court established.   

•   Independence of Judiciary.

Joined UNO- 1971

1981-DYT

·         Shifting the policy-making from the center to district level.

1991-GYT

·         Decentralization down to the grass-root level.

·         Ensured greater people’s participation.

1998-Cabinet

·         Gave his full executive power to the Cabinet

·         JYT

November 2001

·         Commanded the drafting of the Constitution.

March 2005

·         Released Draft constitution.

31^st December 2005

·         ECB established.

9^th December 2006

·         Fourth King stepped down

31^st December 2007

·         NC elections for fifteen Dzongkhags.

29^th January 2008

·         NC elections for five Dzongkhags.

24^th March 2008.

·         National Assembly Election.

·         DPT  won the election.

·         History of democracy

·         42 international observers.

·         107 journalist from 63 media agencies

·         207 reporters from 7 Bhutanese media

·         Unique transition to democracy; peace and harmony

8^th May 2008

·         Meeting of the  MP

·         Fifth King Addressed the House.

ACHIEVEMENTS:

·         Constitution adopted on 18^th July 2008

·         Centenary Celebrations.

·         Coronation of the fifth king.

·         GNH gained the forefront.

·         Supreme Court established.

·         National Judicial Commission established on 15^th March 2010

·         16^th SAARC Summit to be held in Bhutan; CLIMATE CHANGE.

SHORTCOMINGS:

•        CDG in the name of MP.
•       Party President has taken into consideration.
•        Withdrawal of Members.
•        Women representation